Read the previous blog post Towers of Hanoi, then answer the question,” how many cuts does it take to divide a strip of paper into 4 parts, 8 parts, 16 parts?”
Likewise, how many jumps does it take to get from the first entry in our lists of code to the last entry? Answer: obviously, it takes one less than the number of entries in the list.
Observe the pattern of “jumps” required if one starts with a Gray’s ordered set of binary codes and attempts to count in binary. We find that as we deal with longer and longer sequences of codes a pattern of complement and append appears in the sequence of jumps.
The basis sequence is given by what it takes to reorder the foundational 4-bit sequence of parent/child branching in the DD tree…the sequence where we “twisted” every other 0-1 branching in the Binary tree…

To “undo” that twisted DD order we see that to count in the usual order we make jumps of 1, then 2, then -1…1 > 2 > -1 (where we think of the jumps as being oriented as in the graphic above: we start at the top and + is down and – is up).
The sequence required to “undo” the 3-bit DD coding starts with the same sequence as the 2-bit version, but then has a big jump that is followed by the 2-bit version in reverse…
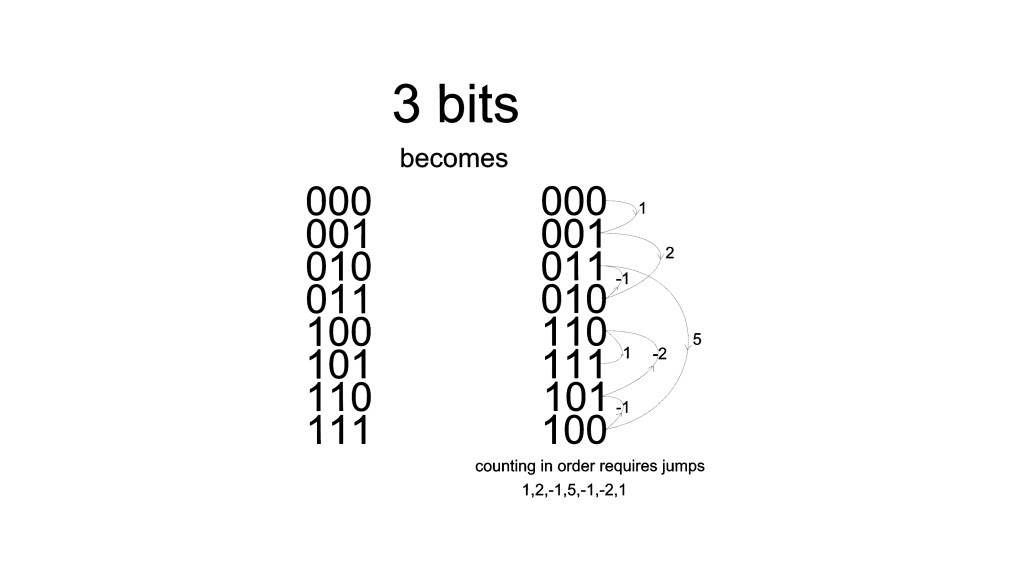
1st sequence 1 > 2 > -1, then reverse…-1 > -2 > 1 then append (or the fancier word: concatenate) with the big jump in between….1 >2 >-1 > 5 > -1 > -2 > 1. The big jump is given by the difference between the number of total jumps in the list (always 1 less than the number of entries in the list) and the sum of the jumps in the sequence from the previous shorter list. In the 3-bit case there are 8 entries -> 7 jumps and the sum from the 2-bit case was 2…1 + 2 + (-1) = 2… so we find the big jump in the 3-bit list is 5.

4-bit has 15 jumps, the sum of the jumps from the 3-bit list is 5, so the big jump should be 10….and so it is. The pattern is set. We start with the sequence from the previous shorter list, construct its reverse sequence and then append with the big jump in the middle.
This structure suggests that we should construct a new tree (let’s call it the anti-DD tree) derived from the DD tree by starting with the distinctive DD row branching 0_1_1_0 and then put that same branching sequence in the left half of the next row followed by its complement. That way our new parent/child branching pattern will do to a code list what we see is necessary to count in the usual order. Only it will do it all at once…it’s a tree after all…the “leaves” all sprout at the same “time”….at the bottom of the tree.
We get this for the branching in the next row in our anti-DD tree: 0_1_1_0 || 1_0_0_1. Then we continue by inserting that sequence of branching in the left half of the next row followed by its complement: 0_1_1_0_1_0_0_1 || 1_0_0_1_0_1_1_0 and so on down the rows of our tree and voilà…we get the anti-DD tree that takes a coded sequence from the DD tree and tells us what path coded from the Binary tree produced it.
The anti-DD tree is the critical member in a trio of automorphisms of the Binary tree. Its branching is the antidote to the “twist” put into the usual counting sequence by the “twisting” of every other parent’s branching in the Binary tree. The structure of the anti-DD tree is significantly different from that of the other two…its branching pattern is not static , but rather is iterative in the sense that each row’s parent/child branching pattern depends on the structure of the previous row and is not determined from the start. There is a pattern as described above, but row to row it is not simply “double the length of the row by copy and append” as in the Binary and DD trees. Instead there is a complement step in between: copy, complement, append.
That copy, complement , append sequence is the fundamental structure to the automorphism group of binary strings. We start with 0, then get 0_1 (Binary tree), then 0_1_1_0 (the DD tree) , and finally 0_1_1_0 || 1_0_0_1. It is fundamental to understanding the structure of “R”, the set of all binary sequences both finite and infinite. Self-similarity with complementation…those two “operators” are the basis elements in the whole structure. All the complexity of “R” is a result of their interaction. That interaction can be described….it is the automorphism group of the three trees.