Towers of Hanoi

Check out this link to the On-Line Encyclopedia of Integer Sequences…

https://oeis.org/A000975

There you will find all kinds of info related to the sequence 2,5,10,22,42,85,170,341,…

The sequence is related to the discrete derivative/Gray’s coding that is the output of the DD tree. When examined closely the transformation of the order of the binary coding found in individual rows of the Binary tree effected by transforming its structure to that of the DD tree (01_01_01_01_… -> 01_10_01_10_…) gives the ordering we find in the rows of the DD tree. That reordering amounts to a series of positional jumps. See below….

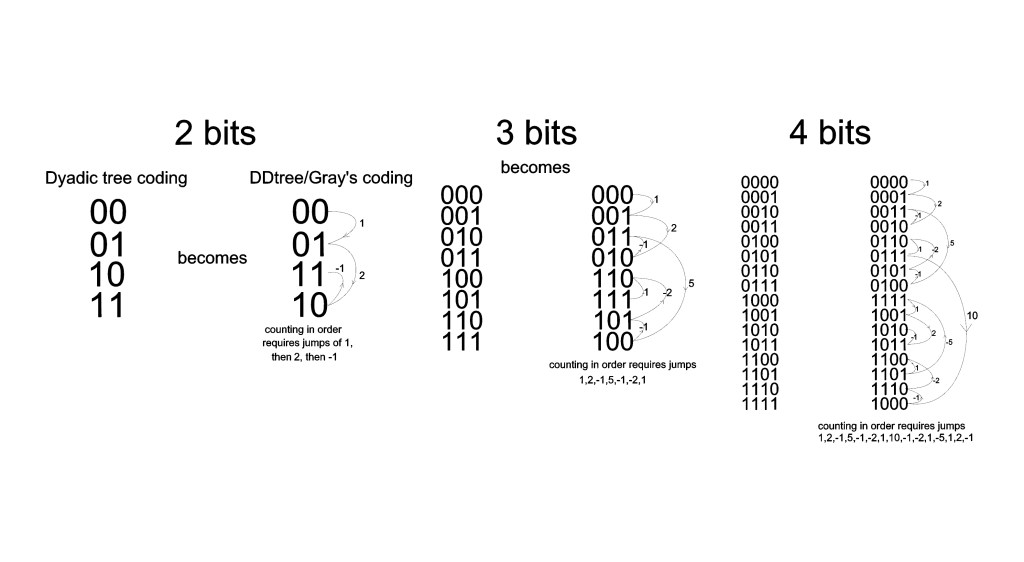
The sequence of maximum jump size grows with the rows of the DD tree according to the sequence given at the link above…2,5,10,22,42,85,170,341,… That sequence is given by a recurrence relation: Starting the row count at 0 for the row 00, 01, 11, 10 in the DD tree, if the row number n is even then the maximum jump in row n+1 is twice that of row n. …that is, calling the max jump in row n “j”, if n is even the max jump in row n+1 is 2j. If n is odd, then the max jump in row n+1 is 2j+1. So the since the max jump in row 0 (the row 00, 01, 11, 10) is 2, then the max jump in the next row (row number 1) is 5, then in row number 2 it is 10, then in row 3 it’s 21, then 42, and so on…exactly the sequence A000975.

If you look closely at the table above you will also see that the reordering is given by a reflection and append type growth…each stage is contained in the next stage along with its “complement”…it is a kind of self-similarity at work. It is a fractal structure much like the Cantor function, the Minkowski ? function, the Weierstass function, etc. Characteristic of these functions is that while they are continuous they lack a derivative either everywhere or at significant points….their “growth” cannot be linearized. The same can be said for the Binary tree: it’s structure cannot be linearized. Hence we see via the linearly ordered table in Cantor’s “diagonal proof” that R cannot be linearly ordered.

The usual (and original) interpretation given to the fact that the code corresponding to the complement of the diagonal cannot be found in the list is not an accurate characterization of the consequent. It is not that “R” cannot be counted. It is that you cannot get a bijection to N via a linear ordering of N and “R”. Self-similar structures can defy linearization while being continuously “countable”. In fact their self-similarity implies a countability…they grow at smaller and smaller scales (countably smaller) in a fixed way by discrete (countable) steps found in a recurrence relation or fixed set of operators. A countable collection of countable steps/sets is countable.

There is no “magic” explosion of points (at infinity) that produces an uncountable set of discrete points from a sequence of segments (the Cantor set construction). Rather, both “R” and the Stern-Brocot tree that models “R” grow in a very orderly way. That process is as follows…

• Since in projective space every point is an “ordinary” point even the points on the line at infinity are just ordinary points.
• Any point (given homogeneous coordinates) can be transformed via a projective transformation to a point at infinity.

So let’s do this…

1. In the projective plane pick a point (call it the “seed”)
2. Consider it as a point on the line at infinity (we can do that in projective space).
3. That means at least two parallel lines meet there (in the projective plane parallel lines meet at a point at infinity…on the line at infinity)
4. Now there exists a transversal of those two lines (other than the line at infinity) that picks a point on each one.
5. Consider that transversal the line at infinity (like points, any line can be transformed into the line at infinity via a projective transformation)….now we have two points on the line at infinity.
6. Repeat: at each of those two points there is an intersection of two parallel lines…now we have four lines.
7. There exists a transversal of those four lines that picks a unique point on each one.
8. Back to 7. Except now we have four points on the line at infinity.
9. And so on.

It is the point/line duality of projective space that makes possible the step-by-step construction of the points on the line at infinity…there is no “magic” explosion. The growth is the consequence of a 2:1 relationship between points and lines….two points determine a unique line (the line with which they are both incident) and two lines determine a unique point (their point of intersection). It is not a coincidence that the Binary tree is also built by a doubling operation.

We get from the discrete to the continuous just the way calculus says we do: via infinitesimal steps…countable infinitesimal steps. The recurrence relations or set of transformations operate at an infinitesimal scale to produce what we see at a larger, “visible” scale. They operate in projective space to produce what we see in affine space.

The countability of “R” is seen by realizing the relationship between the Binary, DD and anti-DD trees. It is the transformation of order of the collection of binary strings via the transformation of structure in those trees that shows it. All three trees are models of “R”, modeled as the set of binary strings (those strings in the Stern-Brocot tree give us the indices of the continuous fraction representation of R). Finally, the three trees are related and are built via the infinitesimals a=[[00][10]] and b=[[01][00]] that are at the foundation of the modular version of the Stern-Brocot tree.

The 00000…string (the infinite string of 0’s) is the fixed point of the DD and anti-DD trees. It runs down the left side of all the trees and is never “relocated”.