The Stern-Brocot Tree

The Stern-Brocot Tree starts with “virtual vertices” (labeled 0/1 and 1/0 below) appended to the basic binary tree structure…

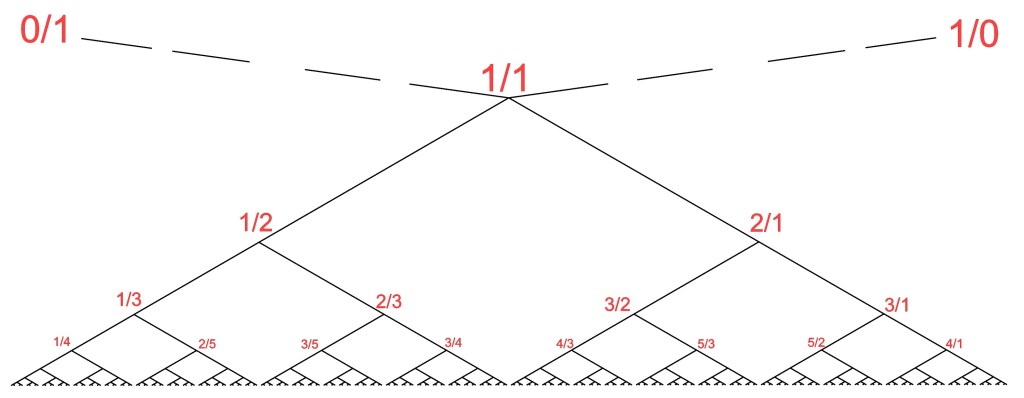
Labels are constructed/assigned via a “mediant” process…add the numerators and denominators of the vertices on each side above the vertex…

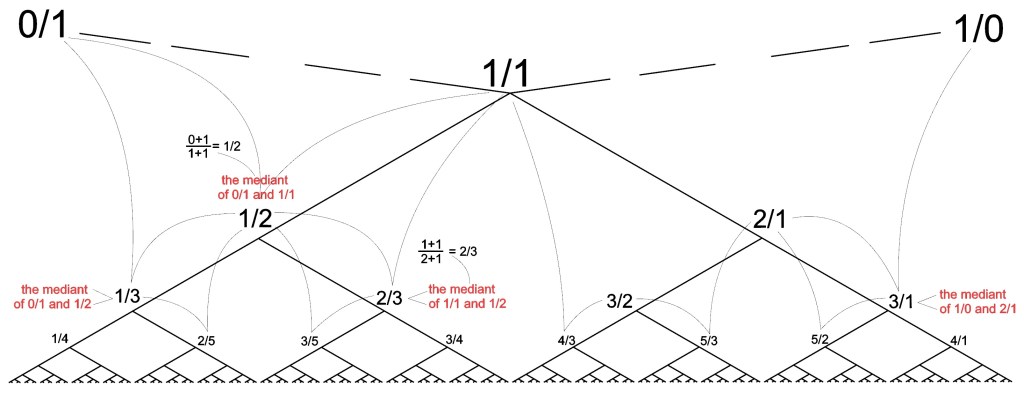
The fact that we can use information from only the previous row without reference to any vertices from other rows will show up again in constructing other label sets for the binary tree structure. The recursive process for labeling the S-B tree involves copy and reflect (mirror) steps that will be important parts of recursive processes for producing other label sets.

What is special about the S-B tree?

1. All fractions are in lowest terms…numerator and denominators are prime to each other.
2. Each fraction is the lowest-terms representative of a whole equivalence class of fractions… all the fractions that are equal to it in value.
3. Every such equivalence class is represented by a label for a vertex in the tree.
4. As a fraction can be thought of as the slope of a line or the tangent of an angle, we can think of the S-B tree as containing all possible rational tangents for angles with respect to the x-axis determined by vectors in the first quadrant of the Cartesian plane.
5. It is important to note that if we refer to a mediant as r/s and either one of its predecessors as p/q we see that |rq – sp| = 1 for every fraction in the tree. That quantity rq – sp will show up in the next tree, the dyadic monoid tree, as the determinant of a 2×2 matrix.