Collatz Proof

Consider the positive integers in base 2, in binary notation.

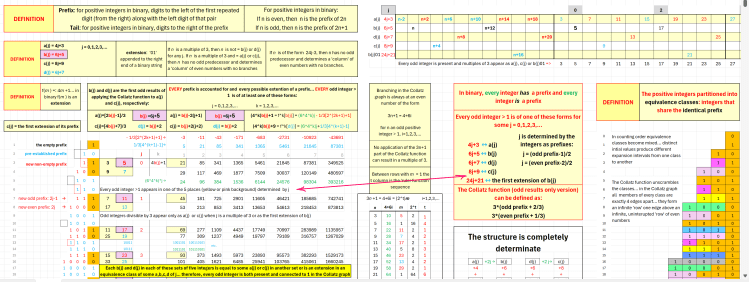
Define prefix: the digits left of the first pair (from the right) of identical digits along with the left digit of that pair.

Define tail: the digits to the right of the prefix.

Define the Collatz function:

Consider the positive integers in binary in counting order. Let e represent the empty prefix. The sequence of prefixes is: e, 1, 10, 11, 100, 101, 110, 111, 1000, 1001,… (see the above file or screen snip). The integers that share a given prefix form an equivalence class. The elements in each class are ordered by string length. Example: the class with prefix 11 in order is 111, 1110, 11101, 111010, 1110101,… Those equivalence classes partition the integers.

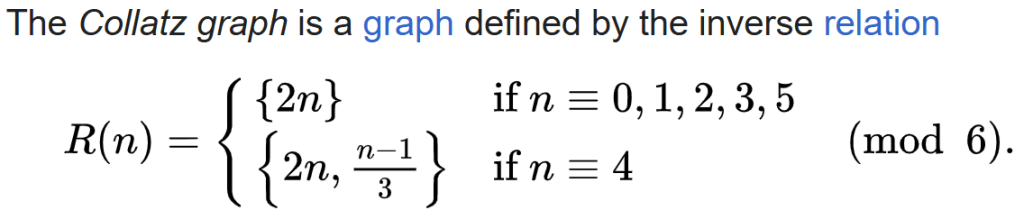
(both above definitions: https://en.wikipedia.org/wiki/Collatz_conjecture)

In what follows we consider only the odd number results of the Collatz function. The even values follow from the odd values.

In a linear array of positive integers in counting order the separation between integers in a class grows exponentially . For example, the elements in the class with prefix e appear in positions 1, 2, 5, 10, 21, …(in binary: 1, 10, 101, 1010, 10101,…) Consecutive odd elements in counting order are separated by a distance given by the usual absolute value of their difference. Consecutive odd element values in the e class are related as e(n+1) = 4*e(n) + 1. The odd elements in every class are related in exactly the same way.

In the Collatz graph the odd elements of every class are separated by a constant four edges. The even elements are separated by 6 edges. In a linear array of integers in counting order elements of different prefix classes are presented as a confused mixture. The Collatz function transforms that confused mixture into an ordered array in the Collatz graph.

In the Stern-Brocot tree encoded in binary (L => 0, R=> 1) each integer class determines an ordered sequence of convergents along the path to one of the irrational elements greater than 1 in the extension field Q(sqrt5). Those paths all share a defining feature: a finite prefix followed by an infinite alternating tail. The equivalence classes of positive integers are in one-to-one correspondence with the irrational elements > 1 in the extension field Q(sqrt5) by way of the binary encoding of the Stern-Brocot tree. That correspondence guarantees that every integer is somewhere in the Collatz graph (can be reached from 1 by the inverse Collatz function). It also is the necessary proof that every positive integer will eventually arrive at the first string in the class with the empty prefix, at 1, with an iterative application of the Collatz function. Every such iteration will halt at the class with the empty prefix….the infinite tail of alternating digits.

Stated in a way that reflects what we see in the diagram above (see the file or the screen snip): The Collatz function takes the chaotic mixture of equivalence classes in the linearly ordered positive integers and filters elements of each equivalence class into a ‘row’. Each ‘row’ is the set of encoded convergents in the Stern-Brocot tree of an irrational > 1 in the extension field Q(sqrt5).

Every such element eventually arrives at an infinite alternating tail.

Every positive integer is accounted for since the foundation of the whole diagram is simply counting in binary. The pattern is fixed.